智猩猩AI整理
编辑:卜圆
仅权重量化的后训练量化(PTQ)是一种广泛应用的技术,通过将LLM的权重压缩为低比特表示,有效降低内存占用并提升推理速度。然而,权重和激活中普遍存在的异常值往往会引发显著的量化误差,导致模型精度明显下降——这一问题在当前强调复杂推理能力的大模型中尤为严重,因为微小的误差会在多步推理过程中不断累积,最终影响整体输出质量。
现有 PTQ 方法要么无法充分抑制异常值,要么在推理阶段引入显著的计算开销。为此,NVIDIA联合加州大学圣迭戈分校提出了成对旋转量化(Pairwise Rotation Quantization, ParoQuant)。该方法融合了硬件友好的可优化 Givens 旋转与通道级缩放,有效均衡了各通道间的数值幅度,并显著缩小了每个量化组内部的动态范围,从而大幅缓解由异常值引起的量化误差。此外,英伟达还协同设计了专用的推理内核,充分挖掘 GPU 的并行计算能力,确保旋转与缩放操作在运行时保持轻量高效。
实验表明,在 4-bit 线性量化这一特定类别中,ParoQuant 在多个主流大语言模型上达到了SOTA,优于此前所有同类方法;在推理任务上相比 AWQ 平均提升 2.4% 的准确率,同时额外推理开销低于 10%。这一成果为在现代 GPU 平台上高效、高精度地部署复杂推理型LLM开辟了新路径。

论文标题:
PAROQUANT: PAIRWISE ROTATION QUANTIZATIONFOR EFFICIENT REASONING LLM INFERENCE
论文链接:
https://arxiv.org/pdf/2511.10645
01 方法
量化与旋转可以通过不同策略平衡计算效率与量化误差,研究团队发现通过仅优化大幅度差异的通道对,能够减少冗余参数,同时保持旋转的有效性,为参数高效的旋转设计提供了新的思路。
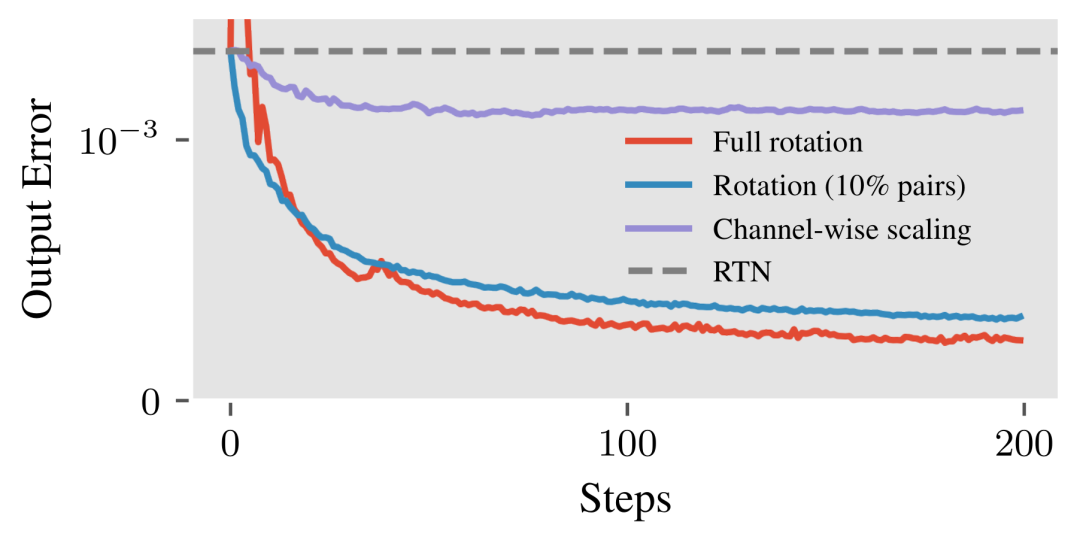
图2 针对 LLaMA-3-8B 模型第一层中 k_proj 权重矩阵,优化变换以最小化量化引起的输出误差所得到的损失曲线
如图2 所示,旋转在降低量化误差方面优于通道级缩放,并且仅保留幅度差异最显著的 10% 通道对进行旋转,其表达能力与完整旋转相当。
(1)带缩放的成对旋转
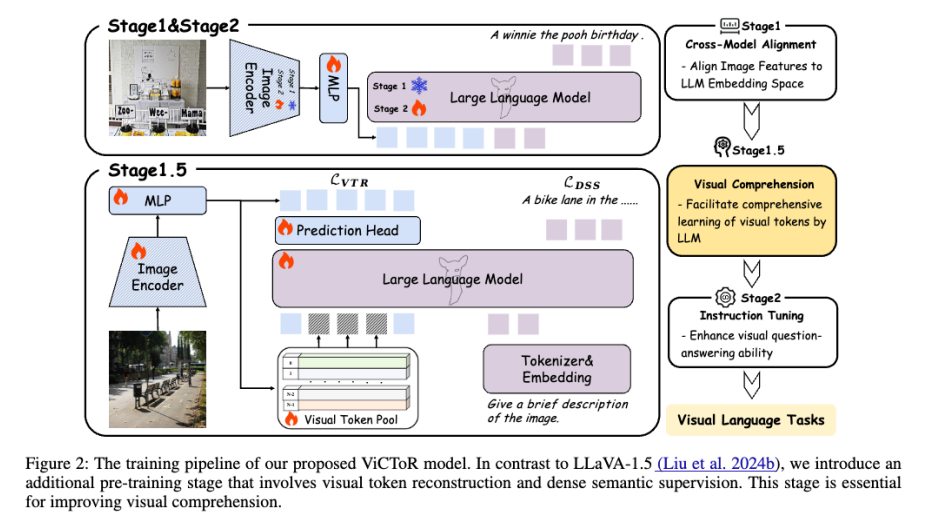
缩放配对旋转变换分为三步:首先,通过用分解的Givens旋转代替正交矩阵,避免直接的矩阵乘法。接下来,消除这些旋转之间的依赖关系,以便在GPU上并行执行,从而实现独立旋转。最后,由于单一的独立旋转不足以有效地拟合复杂的权重分布,所以依次应用一系列独立旋转,并结合通道级的缩放,以提高拟合能力。
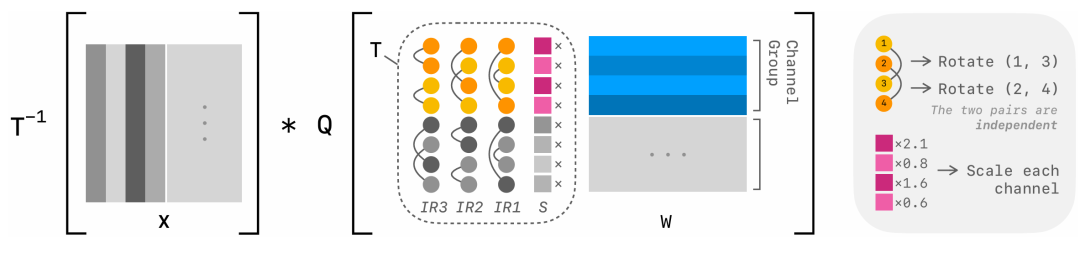
图3 带缩放的配对旋转流程图
如图3所示,通道维度被划分为固定大小的组(图中组大小为4)。每个权重组(W)首先通过通道级缩放(S)进行变换,然后经过一系列独立旋转(IR)。每个独立旋转由相互独立的配对旋转组成。在变换后,应用量化(Q),其组大小与通道组大小相等。逆变换(T⁻¹)应用于激活值(X)。
1)Givens旋转
选择一组通道对P = {(i1, j1), . . . , (im, jm)},并依次旋转 P 中的每一对。形式上,给定 P、旋转角度集Θ = {θ1, ..., θm}以及权重矩阵 W,变换后的权重为:
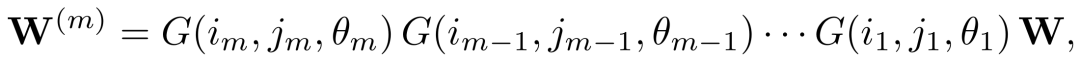
其中 G(ik , jk , θk) 是一个Givens旋转,它仅对矩阵中的第 ik 行和第 jk 行进行旋转,而保持其余行不变。
2)独立旋转
Givens 旋转不满足交换律,其执行顺序会影响结果。因此,存在依赖的 Givens 旋转必须串行计算,无法充分利用 GPU 强大的并行能力,导致显著的延迟。为解决这一问题,研究者令旋转对集合 P 中的所有配对相互独立,即每个通道最多只能出现在一个配对中,使得集合 P 中的所有 Givens 旋转均可完全并行化。
除了计算效率外,独立旋转的另一个优势在于其与分块量化(block-wise quantization)天然兼容,可以利用分块量化中组间的隔离性,为每个组分别应用独立的旋转,这使得每个组都能独立进行细粒度的通道配对,从而进一步提升并行度。
为了解决单次独立旋转表达能力不足的问题,研究团队提出在推理时连续应用少量(比如 8 次)独立旋转,并将它们融合成一个高效计算核。每次旋转随机选择尚未用过的通道对,确保各次旋转之间不重复、保持独立性。这样做既提升了模型的表达能力,又几乎不增加计算开销。
3)结合通道级缩放
在一系列独立旋转的基础上,进一步引入逐通道缩放,以更有效地降低量化误差。由于独立旋转仅作用于有限数量的通道对,其本身难以全局均衡所有通道的数值幅度。逐通道缩放能够直接调节整个矩阵中各通道的尺度,对于弥补独立旋转表达能力的不足、逼近完整旋转的效果至关重要。此外,相比 Givens 旋转,逐通道缩放也更简单高效地抑制孤立的异常值(outliers)。
在结合独立旋转与通道级缩放后,量化前应用于权重的最终变换为:
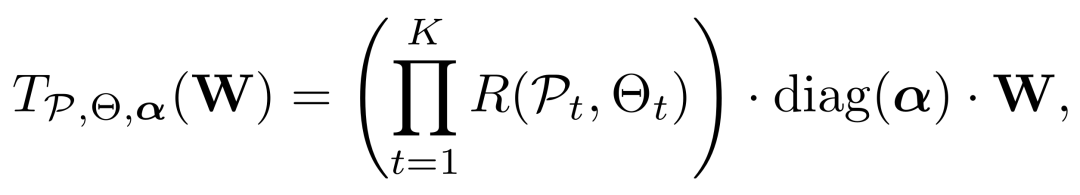
其中,K表示旋转次数,P={P1,...,PK}和Θ={Θ1,...,ΘK}分别是相应的旋转对和角度集合,R(Pt , Θt)是第t个独立旋转,α是每通道缩放因子集合。
(2)层级优化
该优化分为两个阶段:第一阶段联合优化独立旋转和逐通道缩放,有效抑制权重中的大部分异常值,使权重分布更利于量化;第二阶段则借鉴量化感知训练(QAT)的思想,对权重及线性量化参数进行微调,进一步缓解 Round-To-Nearest(RTN)算法带来的残余误差。这一两阶段流程兼顾效率与精度,显著提升了量化模型的整体性能。
(3)高效 Transformer 算子的协同设计
为了加速推理,将缩放成对旋转(scaled pairwise rotation)这一变换操作实现为一个高度优化的融合 CUDA 核函数(fused CUDA kernel),并充分利用其在三个粒度上的天然并行性:在 token 维度上并行处理不同输入序列,在通道组维度上为每个组分配独立的 CUDA block,在旋转对维度上由单个 CUDA 线程负责一对通道的旋转计算。
这种三级细粒度并行设计带来了显著优势:首先,由于通道组规模较小(如 128),激活值可完整载入片上共享内存,而旋转所需的配对索引和角度参数则直接驻留在寄存器中,从而大幅减少高延迟的全局内存访问;其次,通道分组显著增加了活跃线程块的数量,尤其在通道数很大时能更充分地占用 GPU 计算单元;最后,组内各旋转对彼此完全独立,无需线程间同步,进一步提升了硬件利用率。如图4所示,缩放后的成对旋转相对于Hadamard变换速度提升。
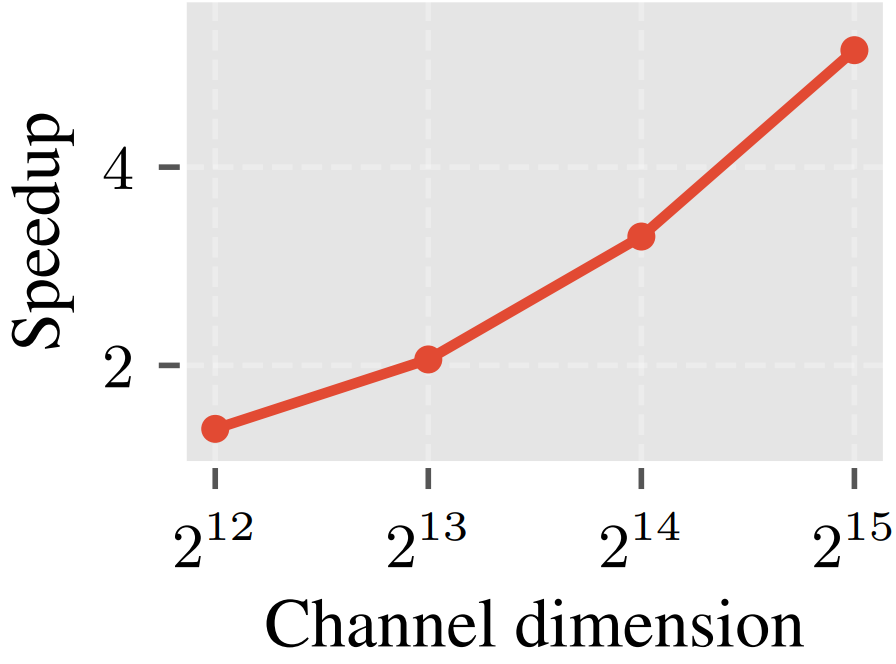
图4 缩放后的成对旋与Hadamard变换的速度对比
02 评估
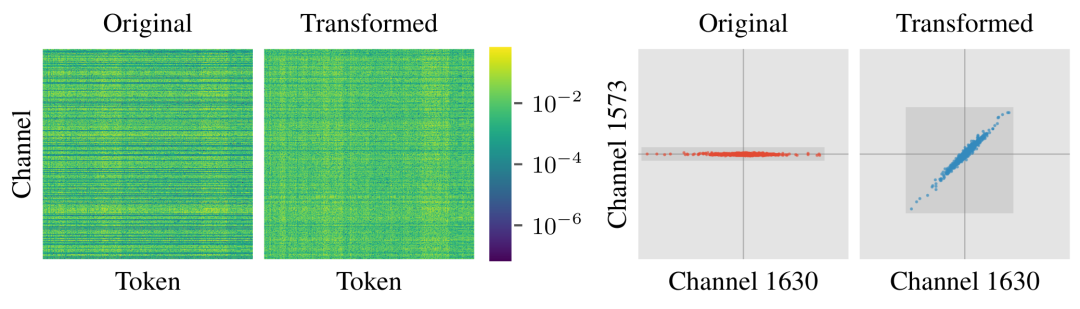
图1 优化的通道级别缩放和旋转效果,左图展示了LLaMA-3-8B第一层的k投影权重在变换后异常值通道得到了有效去除。右图则呈现了权重矩阵中两个通道的散点图,不同通道的值在每个token上更加接近,呈现出沿x = y线聚集的趋势。
(1)精度结果
1)困惑度
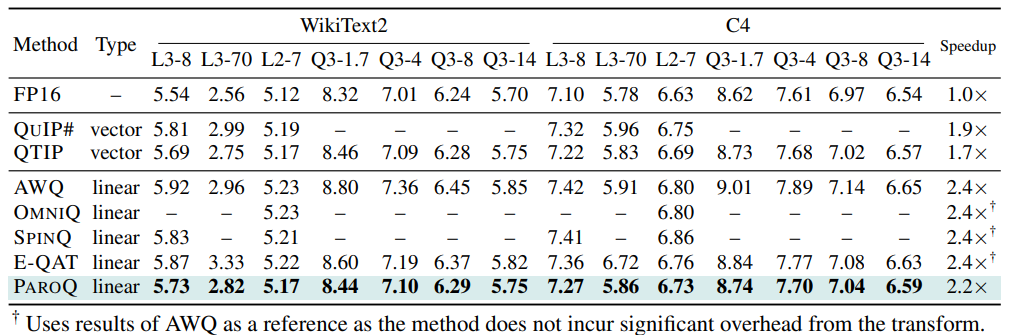
如表1所示,在线性量化方法中,ParoQuant实现了SOTA。在所有尺寸上均表现出高精度,尤其是在LLaMA‑3和4B以下的较小模型等具有挑战性的模型上。
ParoQuant与基于旋转的方法(包括 QuIP#、QTIP 和 SpinQuant)的对比中也表现出色,在所有模型上优于 QuIP# 并与 QTIP 持平。此外,ParoQuant 相较于这两种方法提供了显著的加速效果。
表1 4位量化模型的困惑度结果
2)推理任务
表2展示了在四个推理基准上的准确率结果:MMLU-Pro(12,000个样本)、GPQA Diamond(198个样本)、AIME-24(30个样本)和AIME-25(30个样本)。在规模较大的MMLU-Pro基准上,ParoQuant始终优于所有线性量化基线,并达到了与QTIP相当的准确率。尽管GPQA和AIME等较小基准由于样本量有限,结果表现出一定的随机性,但ParoQuant在大多数情况下仍优于现有基线方法。
总体而言,ParoQuant仅带来平均0.9%的准确率下降,并在EfficientQAT、AWQ和QTIP基础上分别实现了6.5%、2.4%和0.9%的性能提升。这一结果充分验证了ParoQuant在长文本生成任务中优异的量化精度优势。
表2 推理任务的零样本准确率
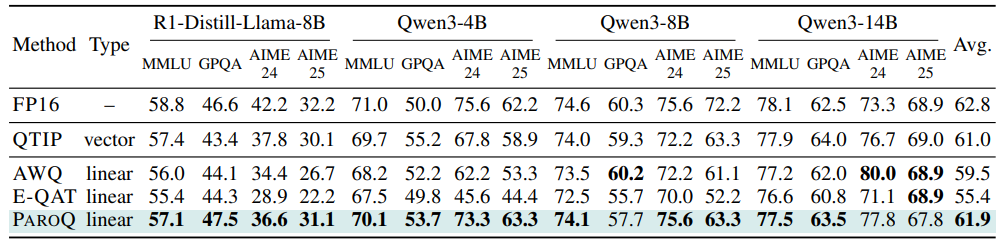
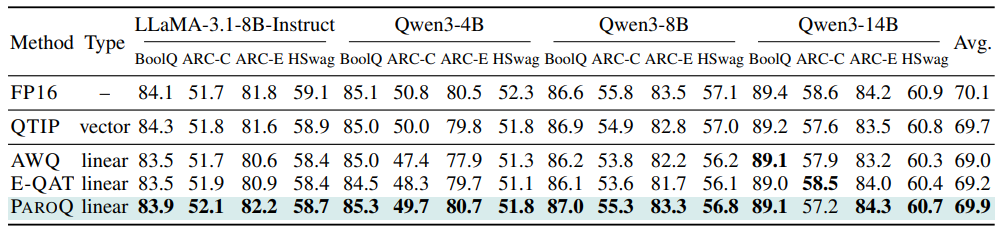
表3展示了在关闭思维链模式下的常识基准上的零样本准确率。ParoQuant保持近乎无损的性能,分别比AWQ、EfficientQAT和QTIP高出0.9%、0.7%和0.2%。由于这些基准仅评估少量生成的词元,误差累积极小,因此准确率差距较推理任务更小。
表3 非推理任务的零样本准确率
(2)效率结果
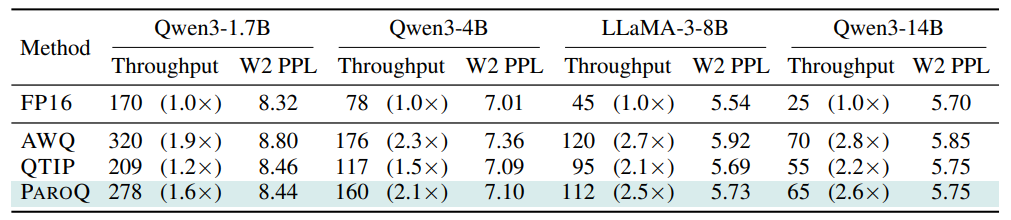
表4展示了ParoQuant在RTXA6000上的解码吞吐量。ParoQuant 仅比 AWQ 慢约 10%,却带来了显著的准确率提升;同时,它在准确率上与 QTIP相当,但推理速度提升了15%-30%。值得注意的是,Qwen3-14B获得了最大的推理加速收益,相较FP16 实现约2.6 倍吞吐量提升,同时保持近乎无损的生成精度。
表4 解码吞吐量(token/s)









 智猩猩AI
智猩猩AI